In A World Without Inertia

Of all the things 2020 has thrown at us: murder hornets, fire tornados, a global pandemic…the one thing it doesn’t have is inertia.

Hear me out. There is no “we’ll just do things the way we’ve always done them” now (though not for lack of trying in some cases).

Everything is new, everything is broken, everything is different.

This has opened the door for the option to not only throw out the baby with the bathwater, but also the entire damn tub.

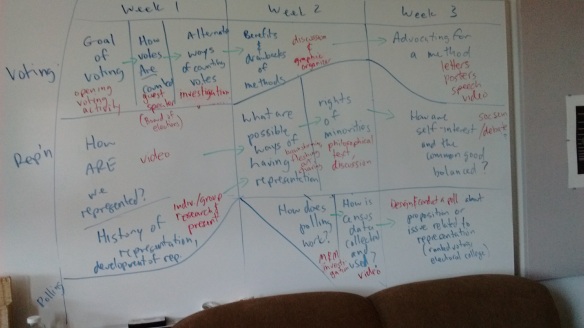
My amazing course team has decided to ask the question:

• What would we do if we didn’t have to cover anything?
• What would happen if we totally reimagined how our math class looked and felt?

These are some of the answers we’re (still) working on:

Syllabus as values statement (I wish I could remember who tweeted that phrase; it rang in my ears for days and I shared it with my team.) This is a paragraph from the document one of our team members came up with, which I *love* more than I ever imagined it was possible to love a syllabus!

“To promote equity and combat white supremacy culture, as well as in recognition of the diversity of challenges experienced differently by different people during this pandemic, we will anchor our grading methodologies with the question, “Does it matter where students started?” We want students to demonstrate growth, to challenge themselves, and personalize their learning. So, our grading methods will try to reflect those core learning principles.”

Rubric of core competencies (Speaking of grading…this is the rubric we’ll be using to assess students)

5 Competencies Rubric

We haven’t quite figured out how we’re going to translate all that into a letter grade yet. Given that all of us on the team are proponents of abolishing letter grades, this will definitely be our biggest challenge. The only thing we do know is that all of a student’s graded work (and much of their ungraded work) will go into a semester-long Process Portfolio, made in Google Slides, which we’ll discuss regularly, both via 1:1 conferences and in written notes/reflections/feedback in the speaker notes section.

Intake form (HT to @sheathescholar for their idea to make a google form into a conversation…my intake form emerged directly from that.) Here are the first few questions–only the first question was required.

Music in the Zoom-room (HT to @carloliwitter, @AlainMotaSTEM, @LauraVHawkins, et. al. for their suggestions, pro-tips and playlists) After having been in several sessions that used music as a way to bring everyone into the meeting…and then hearing the awkward silence in one of my own breakout room sessions, I realized this was a must-do. I was given a master-class in finding and playing background music. If you also want tips, go read the thread on Twitter.

Sharing Pronouns (HT to @Alice_J_Grimm for a long-ago post about this that impacted me) I changed my profile name on Zoom so it now includes she/her so students can see my pronouns. I haven’t said anything about this (beyond what I said in my intake form), and I don’t plan on saying anything. I’ve already noticed one student rename himself during my class to include pronouns in his name. No student should feel obligated or pressured into sharing their pronouns with me, but I want to signal that I acknowledge that I don’t actually know what their pronouns are until they tell me. My profile name helps me say that.

Mathematics of Democracy: A Story of Three Weeks (part 1)

Imagine that you had three weeks with a group of ~20 students. You can do WHATEVER you want with them during those three weeks, because you have them all day long. There has to be some academic rigor to your choice, but that is the only restriction. What would you do?

This is what my school asked us to imagine a little over two years ago. We had voted (unanimously, which is unheard of) to move to a semester schedule with two “Immersive” courses, in January and June, during which students would take one class,  equivalent to a one-semester credit. We were encouraged to work together, to dream big and to think about doing things in this course that we couldn’t otherwise do during “business as usual” semester courses.

For a variety of reasons our school decided to wait for two years before implementing the change to a semester schedule (prior to this, we were on trimesters). During those two years we were first asked, in year one, to plan a “practice” immersive course and then, in year two, to write a proposal for a course we wanted to teach the following year a.k.a. the 2018-2019 school year a.k.a. THIS YEAR!

Well, friends, I knew immediately what I wanted to do: Mathematics of Democracy.

The name hadn’t yet been found, but what I wanted to do was a Voting Theory course that explored the math behind elections. A course in which students learned about civics and math. I needed a partner, someone who taught social studies, and luckily I found one in my colleague, Craig Butz.

In year one, we mapped out our course: the essential questions, the arc of the course, how the different strands of representation, voting theory and civic engagement would play off of one another. In year two, we planned in more detail, what a typical day looked like, who would teach what when, what kinds of trips we wanted to go on. We gave ourselves large To Do lists before parting ways for the summer.

And then I had a baby…

So that was cool.

Craig did whatever he did to make sure all of our field trips and guest speakers were arranged for. A parent helped a TON with this too, doing things like putting us in contact with staffs for various city and state elected officials so we could coordinate meetings and finding people who’d worked on the SF city redistricting project in various capacities to create a panel of experts for our students. She even found me a lactation room I could use on our trip to the State Capital! Truly a valuable asset to our course planning process.

Before we knew it, the first day of the course had arrived. Which was also my first day back at work following maternity leave. Teaching an all-day, three-week long course is certainly an…interesting…way to come back into full-time teaching. In some ways it was really perfect, though. Because we had the students all day, we started school later than usual and ended a smidge earlier. Because we were co-teaching, I could leave to go pump whenever I needed to.

However, I’m guessing the Venn diagram of teachers who would love to add Mathematics of Democracy content to their curricula and the teachers who have tiny babies at home is fairly sparsely populated, so I think I’ll move on.

When we initially planned out our course, this is the map we made outlining the big ideas we’d bring in/out/through the course:

As we all know, nothing goes exactly to plan…

But that is the story for a second post.

#TMWYK – Overheard on MUNI Edition

This is from a while ago, but I never #pushedsend

—

Dad: What’s 152 divided by 8?

Girl: …

Dad: …

Girl: 19!

Dad: Great!

*pause during which I bite my tongue*

Dad: How did you get that?

Girl: I did it 20 times and then I realized it was 8 less.

Girl: But first I tried it times 10 and tried to add up.

Dad: That was kind of a slog though, wasn’t it?

Girl: Yeah–

And then I had to get off of the bus.

NCTM 2017 Slides & Handout

NCTM 2017 Beyond Sudoku-Slides

 

NCTM 2017 Handout

 

Week Eleven–More Important Than Math

I want to honor my commitment to posting weekly, but this week I can’t simply report on what happened in my classes. This week was too much. This week was too hard.

I live in the great state of California, in the amazing city of San Francisco. We are by no means universal in our beliefs, political or otherwise, but there is a definite liberal leaning around these parts. Many people in my life are reeling right now from the outcome of the election. I am as well.

Our students were hurting this week. They were confused, they were angry, they were disappointed, some of them were scared. We teach our students to be honest, to be kind, to conduct themselves with integrity in all that they do. They make plenty of mistakes, but they also come to expect this of themselves and of one another. They certainly expected the same from the leaders of our country.

On Wednesdays our school schedule begins with advisory. We meet in small groups that stay together across all four years a student is at our school. This year I have a new (and awesome) group of freshmen. There was a plan–an agenda–for the week, but that all went out the window Tuesday night as the election results rolled in. When I walked into my advisory room on the 9th, one of my advisees was in tears. She’d stayed up late talking and texting with her friends, one of whom is terrified that his parents will be deported.

I can’t just tell these kids that everything will be okay.

I wish that I could. I wish that I believed that this was true. But I just don’t know if it is.

Instead, I asked everyone to check in with how they were feeling. I went first. I shared how I was scared and sad and frustrated and angry and confused. My voice shook and my eyes welled up with tears, but still I spoke. I told my students that I would be looking for ways to stand up and make a difference. To do good in the world in whatever way I could.

Each student shared their thoughts, which ranged from deep sadness to outright confusion and disbelief. Afterwards, I asked everyone to go around and share something they were grateful for. Despite the strong emotions that we had shared with one another, we ended our time together with gratitude. For family and friends; for a future where this group of young people will have more of a voice; for the outcomes in this election that we do celebrate; and for chocolate chip cookies, which were very much needed at that moment in time.

***

The Student Life Council recently put up a blackboard in our dining hall for students and staff to write in response to a variety of prompts. Wednesday’s prompt was “What are you scared of?”

I wrote: Apathy.

Week Ten–A Day Late…

 

Howdy All,

Did you think I’d forgotten to post about last week? Well, sorry to burst your bubble–or rather, happy to give you the goods!

Last week was a little odd. First we had Halloween. I got observed on Monday too. That was fun–no, really; it was! I mean, it’s not every day you get video-taped wearing a chef costume with a banana sitting in the shot. 🙂 And I did great. My students are awesome. ❤

Then, on November 1, our school had a PD day (genius move, btw). Then, I took a personal day on Friday to fly to Palm Springs for the CMC-South conference. The added stress of packing for a trip (with a baby) on top of planning for a sub day (even though I was just giving a test in most classes) was crazy-ville. Also, not a whole lot of school days in there, in case you didn’t catch on.

It was Mara’s first trip to go to a conference–though it wasn’t her first conference. She attended part of the Desmos pre-conference and ShadowCon last year at NCTM. She was a bit more alert this time for her first Ignite session.

How much fun was #ignite at #CMCmath? It was this much fun! @woutgeo @btwnthenumbers pic.twitter.com/ArJxKoZppo

— Annie Fetter (@MFAnnie) November 5, 2016

Poor child. This is her life for the next 18 years.

Okay, okay…at some point we may let her stay home. We’re not monsters.

Though according to Patrick Callahan, we are going to hell.

Week Nine–Step By Step

So, this week my students continued their work with congruent triangles. The thought-process behind this part of the unit has been intentionally moving up from physical/concrete reasoning to more and more abstract and rigorous reasoning. Going step by step along the way.

We started last week by creating and measuring physical triangles in order to establish sufficient criteria for showing two triangles to be congruent. Then, this week we used diagrams of triangles with sides and angles marked to determine whether or not the two were congruent. After we got good at that we moved on to writing proofs that two triangles were congruent. Finally, we added on to that the next day by using CPCTC to prove various things were congruent. By the time we got to CPCTC students were like:

That’s it?

And I was like:

Yep. That’s it.

And they continued to be awesome.

I don’t know what it is that I’m doing right–whether it’s my trust in students’ writing and critiquing skills, or my amazingly coherent lesson planning which allows students to build skills incrementally, or if it’s the insightful feedback I give on student work, or if I just got lucky (again)–but I feel like when I teach proofs, students do well (a feeling that some of my colleagues do not share).

I feel particularly successful this year. And I do think it has to do with the first item on my (somewhat tongue-in-cheek) list up there. The students read and commented on A LOT of proofs over the course of this unit. They saw good stuff; they saw mediocre stuff; they saw some pretty crappy stuff too. And seeing work that is effective, alongside work that isn’t, is one of the best ways that I know to become a better writer.

Turns out it works with mathematical writing too.

Who’da thunk?

***

Also, this week I got a great email from the mom of one of my students, letting me know that her child was really excited about what we’re doing in class and was eager to tell Mom all about it–something that this child apparently doesn’t do very often.

Talk about making my day week!

Week Eight–Trust, But Verify

Our wifi has been on the fritz for several weeks (it seems like the issue may be resolved for the time being, but it was pretty hairy for a while there) which was a pain in the you-know-what. But like all storm clouds, it had its silver lining.

From my first year at my school, seven years ago, whenever I taught triangle congruence I did it using an interactive Geometer’s Sketchpad file that had students manipulate virtual triangle configurations to try to make non-congruent triangles. This year I knew I needed a back-up plan in case the wifi was down and they couldn’t download the document onto their laptops. So it was back to good ol’ rulers and protractors!

Talking the idea over with my office-mate, I decided that I didn’t care whether the wifi was out or not, I was going to do the paper and protractor version anyways.

Kinesthetic learning! Using appropriate tools with precision! Decorating triangles!

The decorating was very important, btw.

I had read this blog post, which for some reason I didn’t clip to Evernote (why?!?), that talked about giving students the following scenario:

Let’s say I ask Suzy to create a triangle with sides measuring 3 inches, 4 inches and 5 inches for homework. Now, I know Suzy is really amazing with a ruler and scissors, so she is going to come back tomorrow with a really great triangle whose sides are 3, 4 and 5 inches long. Let’s say I also ask Stewart to do the same task. Stewart’s skills with ruler and scissors are equally amazing, so his triangle will also be great.

I want to know, will Suzy’s and Stewart’s triangles be exactly the same or could they be different?

The class discussed this, as well as the second scenario, which is the same except that now the triangle being made is 45 degrees, 45 degrees and 90 degrees. Then the teacher threw out another scenario (don’t remember what it was) and kept doing this until a student suggested “Let’s try it!” Then, out came the rulers, protractors and scissors and away they went.

I didn’t wait for students to suggest the cutting–I gave them time to discuss the first and second scenarios and then I had them construct the two triangles, decorate them and cut them out. In my first class I had them tape their triangles to pieces of paper all at the end of class (it was kind of a last-minute thought) but for the second class I had them do this for each triangle as they went along. I taped up papers labeled “1”, “2”, etc. around the room and wrote out the triangle’s criteria next to the paper on the whiteboard. This worked really well; students went up and taped their triangle to the paper as they finished and then they moved on to the next triangle. I was able to take down papers that everyone had finished and put up the new ones as we went along, which helped keep everyone moving forward without having stress to rush through because they hadtofinishinthreeminutesohmygahhhh!

There were multiple (!) exclamations of “this is fun” from (unexpected!) students as they were cutting and measuring and taping and decorating. When class was over we had multiple pages worth of triangles for many of the criteria and a full page worth of all the rest.

That afternoon/next morning I selected triangles to put on the “final sheet”–really I just took off triangles so that there was one page per set of criteria–and photocopied each page. This is where the decorations came in handy. That was my selection criteria–not accuracy, but aesthetics! [also what will show up on a photocopy best]

Day two was our day to come up with some conclusions: Was SAS enough information to determine whether two triangles would be congruent? What did SAS mean, really?

I had students Trust, But Verify one another’s work. Which means I passed out the photocopies of the triangle sheets and check to see whether each triangle on the page satisfied the given criteria. This means students needed to measure the side lengths and angle measures as well as figure out if they were in the correct order. So, not only were students getting additional practice with protractors–something some of them really needed–but they were forced to confront the idea that AAS meant something specific about where the 30 degree angle went and realize that which angle the 5 inch side was touching made a difference.

I didn’t anticipate that this activity would address this misconception, but it did. Big time! Students were figuring out on their own that if the 5″ side was touching the 40 degree angle rather than the 30 degree angle this was not the same triangle as the one that was doing the reverse.

By the end of the class we had a set of criteria for determining triangle congruence.

And I could positively kiss the kid who, when we were talking about SSA, asked:

Isn’t this like that problem we did in our last unit?

 

Yes, little darling.

Yes, it absolutely is.

Week Seven–Feeling Good…

First things first: a little celebration is in order–Mara slept through the night 4 nights this week! Huzzah!! This is the first time she hasn’t waken up in the middle of the night, for multiple nights in a row, since school began. Fingers crossed that we are moving towards a new “normal”.

Perhaps it was (in part) because of the extra hours of sleep, but this week–despite being a full week after a short one–felt good. I had my students fill out midterm course evaluations (anonymously) on Monday. It took me a few days to get around to reading them. I always am a bit nervous about doing this, so I waited for a time when I knew I could decompress afterwards if that was needed. Turns out it wasn’t.

While the comments were by no means universally complimentary (something I appreciate, because that’s not actually helpful!), the students were forthright and constructive in their feedback. It also seemed clear to me that some of the items I’ve been working on (e.g. providing more variety of tasks) has been noticed and well-received by my classes. So that was good. And I got some usable suggestions that I can try to incorporate moving forward. Also good.

***

One of the biggest changes that I see in myself in this year’s version of our proofs unit compared to previous years is that I am doing a good job of shifting the onus of responsibility for checking students’ work from myself as “arbiter-of-accuracy” onto the students themselves. I’ve done several gallery walks where they write comments to one another on the whiteboards about what is effective and what is confusing about their group’s proof. These followed a more structured proof “writing workshop” where they commented (on google docs this year!) on one another’s work and read the feedback from their peers. I’ve done the writing workshop in previous years, but then drifted away from building upon that. This feels so much better!

We did some proof puzzles–I wrote up statements and reasons for some problems and had students arrange them in order–and I got to model what I look for when checking a proof.

First, I check to see: do you have the givens?

Then, I check: did you end with the thing you were trying to prove?

Finally, I check the middle: is each statement supported by the ones that come before it?

This has taken place over the past three-ish weeks, but this past week it really felt like things came together. I had students work on the lovely TIMMS problem below and had different students put up their solution method on the board.

I carefully selected students who used different methods (add a parallel line, add a perpendicular line, extend the lines) so that students could see a variety of ways to solve the problem. [I overheard one student say “I think that’s how we were supposed to do it.” which made me shake my head…your way worked too!!!] Then I gave them additional numbers to work, using a method that was different than their own, until they noticed a pattern and a conjecture emerged.

I wrote the conjecture on the board and asked the class, “What do we do with conjectures?”

Class: “Try to prove them!”

And so they did. Afterwards, they exchanged papers with someone in front/behind them (so as to avoid exchanging with someone they may have worked with) and took 1 minute of silent reading time to look over their partner’s work then they talked it over. The room was abuzz with great conversation! They were helping one another hone their arguments and make things clearer.

It felt good.

Week Six–Freshman Conferences

So, this week was a short week–only two days of classes–due to our annual round of freshman conferences. This year I have freshman advisees, so I was on the hook for 8 conferences, plus one for my lone 9th grader in Math 3A. There’s this strange balance between number of conferences versus number of comments to write which is totally thrown off when you have freshman advisees and (practically) no freshman students. Basically, I have to write comments for all of my students *and* I had to take the time to go to these 9 different conferences. Having a small set of conferences gave me time during the day to get started on writing comments and to do all of my grading, but I was much less productive over Thursday and Friday, not to mention Wednesday, which was a work-day, than I typically am.

I blame Mara.

🙂

I stayed home on Wednesday, though I did have childcare in the morning, which allowed me to do a bunch of grading. But my goal of doing all of my comments for Topology–a class of only 5 students–was stymied by doing such important tasks as: going to the park, making chicken stock, washing all of the dishes. Okay, so only one of those chores was really Mara’s fault.

During the day on Thursday and Friday I went into work from 9 to 2:30 both days. I had quite a bit of free hours on Thursday, not so many on Friday. But this pumping thing, it eats up quite a bit of time…

I was able to finish my grading (and Topology comments) on Thursday. On Friday I wrote a few more comments, but I went off campus during my lunch break to attend a breastfeeding support group I used to go to regularly. That was fun; wish I could have taken Mara.

The upshot to all of this is, I have been writing comments today and have one more class-worth of comments to write tomorrow. And I suppose I should figure out what the heck I’m doing for my classes on Monday at some point.

😛